PyMC set-up

Walk through as per the installation instructions https://www.pymc.io/projects/docs/en/latest/learn/core_notebooks/pymc_overview.html

import arviz as az
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import sqlalchemy as sa

%config InlineBackend.figure_format = 'retina'
# Initialize random number generator
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

# True parameter values
alpha, sigma = 1, 1
beta = [1, 2.5]

# Size of dataset
size = 100

# Predictor variable
X1 = np.random.randn(size)
X2 = np.random.randn(size) * 0.2

# Simulate outcome variable
Y = alpha + beta[0] * X1 + beta[1] * X2 + rng.normal(size=size) * sigma

fig, axes = plt.subplots(1, 2, sharex=True, figsize=(10, 4))
axes[0].scatter(X1, Y, alpha=0.6)
axes[1].scatter(X2, Y, alpha=0.6)
axes[0].set_ylabel("Y")
axes[0].set_xlabel("X1")
axes[1].set_xlabel("X2");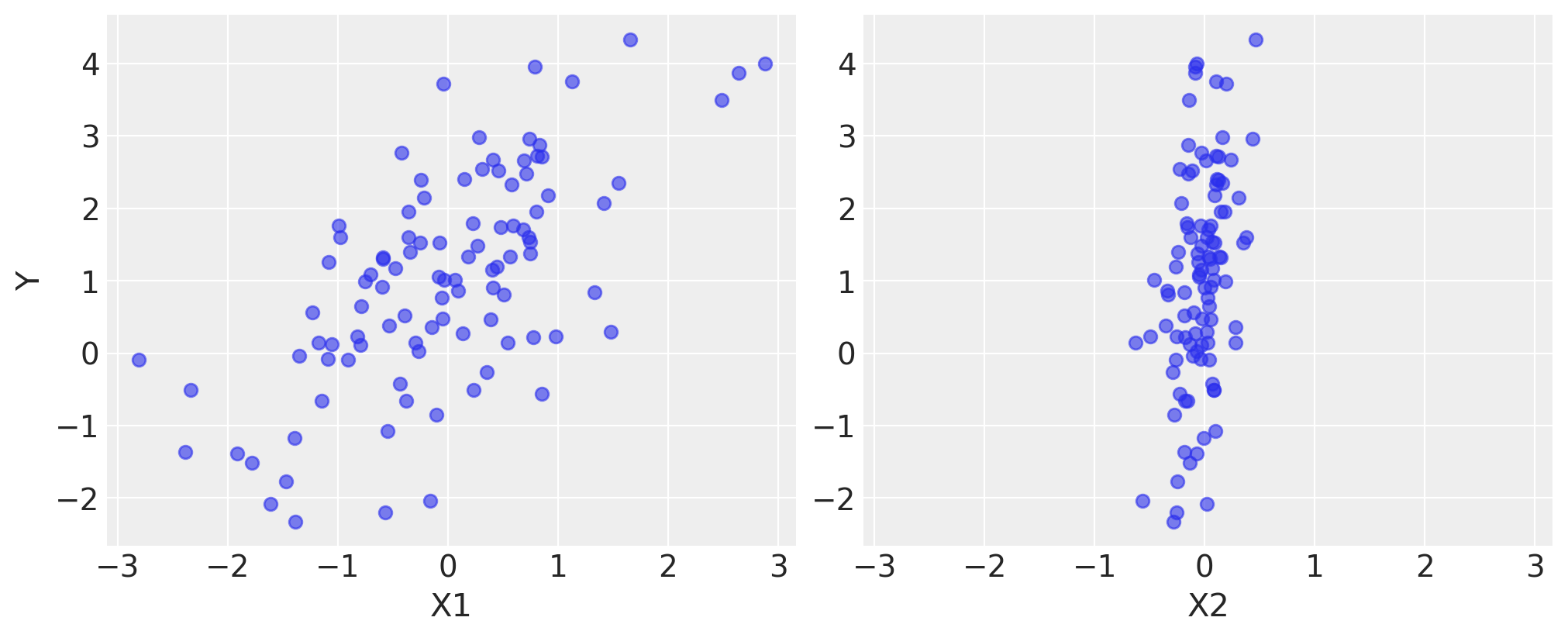

import pymc as pm

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v4.2.2

basic_model = pm.Model()

with basic_model:

    # Priors for unknown model parameters
    alpha = pm.Normal("alpha", mu=0, sigma=10)
    beta = pm.Normal("beta", mu=0, sigma=10, shape=2)
    sigma = pm.HalfNormal("sigma", sigma=1)

    # Expected value of outcome
    mu = alpha + beta[0] * X1 + beta[1] * X2

    # Likelihood (sampling distribution) of observations
    Y_obs = pm.Normal("Y_obs", mu=mu, sigma=sigma, observed=Y)

with basic_model:
    # draw 1000 posterior samples
    idata = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta, sigma]

100.00% [8000/8000 00:00<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 7 seconds.

idata

arviz.InferenceData

idata.posterior["alpha"].sel(draw=slice(0, 4))

<xarray.DataArray 'alpha' (chain: 4, draw: 5)>
array([[1.22182606, 1.06122449, 1.19960544, 1.11622334, 1.17347533],
       [1.33032996, 1.06347311, 1.07428442, 1.12094194, 1.28404611],
       [0.99688654, 1.25084385, 1.05605624, 1.28236762, 1.28115075],
       [1.15648514, 1.09849708, 1.05702968, 1.23564325, 1.16488626]])
Coordinates:
  * chain    (chain) int64 0 1 2 3
  * draw     (draw) int64 0 1 2 3 4

with basic_model:
    # instantiate sampler
    step = pm.Slice()

    # draw 5000 posterior samples
    slice_idata = pm.sample(5000, step=step)

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>Slice: [alpha]
>Slice: [beta]
>Slice: [sigma]

100.00% [24000/24000 00:03<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 9 seconds.

az.plot_trace(idata, combined=True);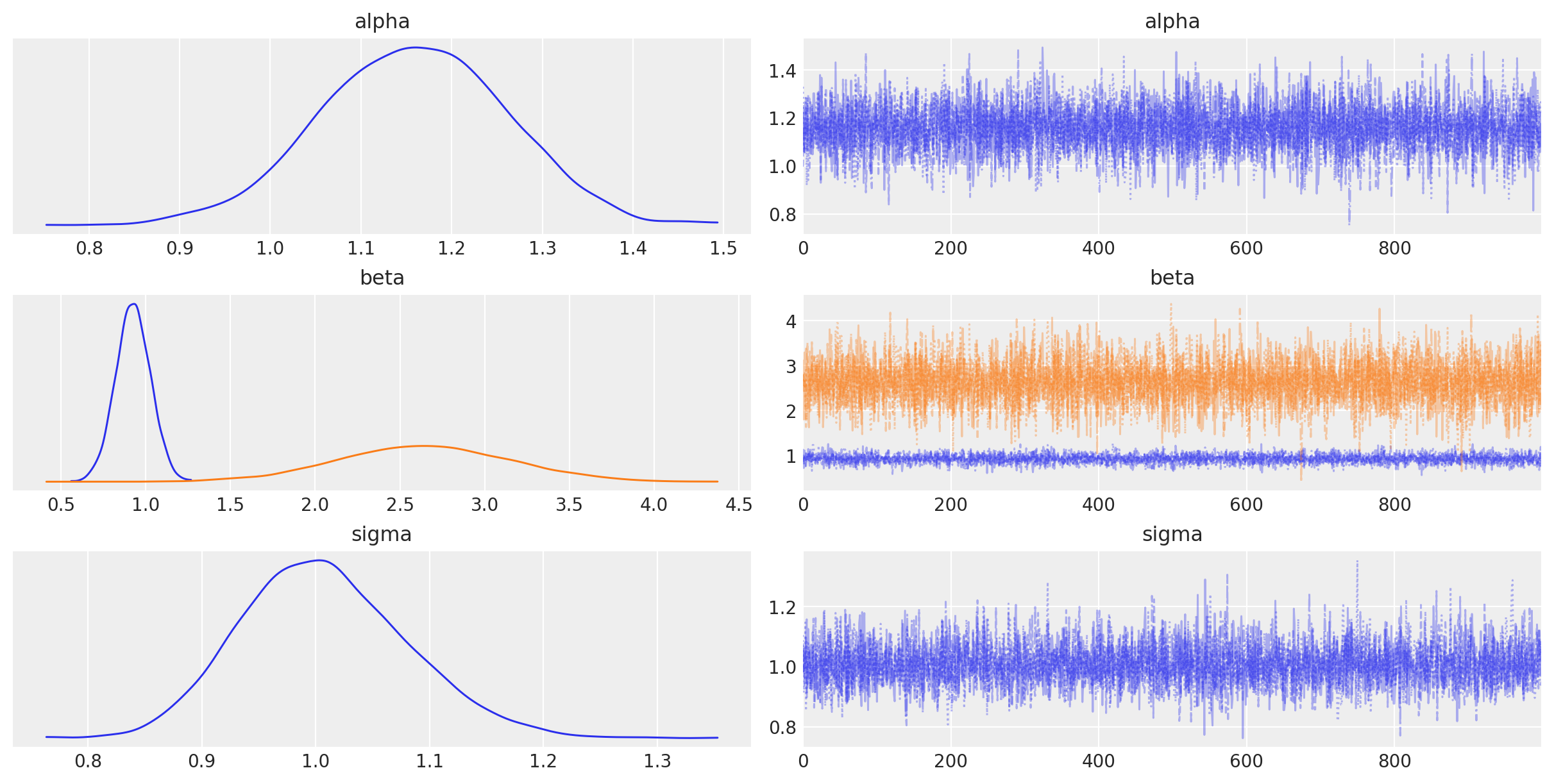

az.summary(idata, round_to=2)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	ess_bulk	ess_tail	r_hat
alpha	1.16	0.10	0.98	1.36	0.00	5564.31	3063.75	1.0
beta[0]	0.93	0.10	0.73	1.12	0.00	5600.72	3264.84	1.0
beta[1]	2.64	0.51	1.76	3.65	0.01	5761.89	3160.86	1.0
sigma	1.01	0.07	0.87	1.14	0.00	5343.73	3051.86	1.0